TIPOS DE FUNCIONES

TIPOS DE FUNCIONES

FUNCIÓN CONSTANTE

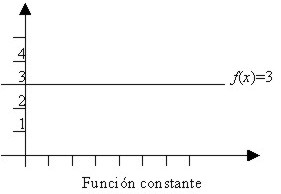
Una función de la forma f(x) = b, donde b es una constante, se conoce como una función constante.

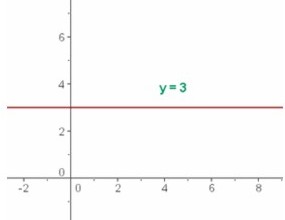
Por ejemplo, f(x) = 3, (que corresponde al valor de y) donde el dominio es el conjunto de los números reales y el recorrido es {3}, por tanto y = 3. La gráfica de abajo muestra que es una recta horizontal.

FUNCIÓN LINEAL

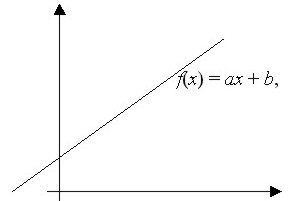
Una función de la forma f(x) = mx + b se conoce como una función lineal, donde m representa la pendiente y b representa el intercepto en y. La representación gráfica de una función lineal es una recta. Las funciones lineales son funciones polinómicas.

Ejemplo:

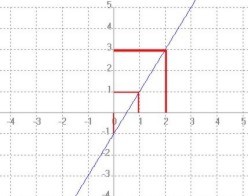
F(x) = 2x - 1

Es una función lineal con pendiente m = 2 e intercepto en y en (0, -1). Su gráfica es una recta ascendente.

Para trazar la gráfica de una función lineal solo es necesario conocer dos de sus puntos.

La ecuación matemática que representa a esta función, como ya vimos, es f(x) = ax + b, donde f(x) corresponde al valor de y, entonces

y = ax + b

Donde "a" es la pendiente de la recta, y "b" es la ordenada al origen.

La pendiente indica la inclinación de la recta, cuanto sube o baja y cuanto avanza o retrocede. Esto depende del signo que tenga.

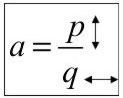
El valor de "a" siempre es una fracción (si no tiene nada abajo, es porque tiene un 1), donde el numerador (p) me indica cuanto sube o baja, y el denominador (q) indica cuanto avanzo o retrocedo.

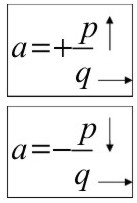
Aprendido esto, y según el signo de la fracción, la pendiente se marca de la siguiente forma:

La ordenada al origen (b) es el valor donde la recta corta al eje y.

La recta siempre va a pasar por el punto (0; b)

Representación gráfica de una función lineal o función afín

Para graficar una recta, alcanza con los datos que da la ecuación matemática de la función, y se opera de la siguiente manera:

• 1. Se marca sobre el eje y la ordenada al origen, el punto por donde la recta va a cortar dicho eje.
• 2. Desde ese punto, subo o bajo según sea el valor de "p" y avanzo o retrocedo según indique el valor de "q". En ese nuevo lugar, marco el segundo punto de la recta.
• 3. Se podría seguir marcando puntos con la misma pendiente, pero con 2 de ellos ya es suficiente como para poder graficar la recta.
• 4. Teniendo ya los dos puntos, con regla se traza la recta que pasa por los mismos.

Ejemplo:

Graficar la siguiente función:

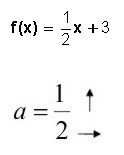
La ordenada al origen (3) me indica que me debo parar sobre el eje y en el 3.

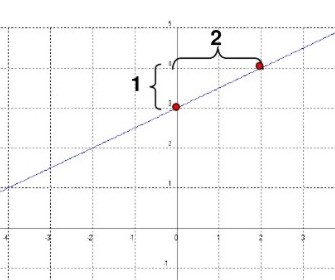
También podemos graficar una función dando valores a x y obteniendo dos puntos en las coordenadas.

Ejemplo:

Graficar  la función dada por  f(x) = 2x – 1

Solución

Como la función es lineal se buscan dos puntos de la recta; para ello, se le dan valores a  x  y se encuentran sus imágenes respectivas, esto es:

                          

    Si  x = 0, se tiene que  f (0) = 2(0) – 1 = - 1

 Si  x = 2, se tiene que f (2) = 2(2) – 1 = 3

Así, los puntos obtenidos  son (0, -1) y (2, 3), por los cuales se traza la gráfica  correspondiente.

FUNCIÓN POLINOMIAL

Una función f es una función polinomica si, f(x)=anx^n+an-1x^n-1+...+a1x+a0

Donde a0, a1,..., an son numeros reales y los exponentes son enteros positivos.

El dominio de todas estas funciones polinómicas es el conjunto de los números reales (porque el elemento x puede ser cualquier número real).

FUNCIONES CUADRÁTICAS

Una función de la forma f(x) = ax2 + bx + c, donde a, b y c son constantes y a es diferente de cero, se conoce como una función cuadrática.

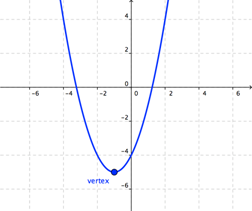
La representación gráfica de una función cuadrática es una parábola. Una parábola abre hacia arriba si a > 0 y abre hacia abajo si a < 0.  El vértice de una parábola se determina por la fórmula:

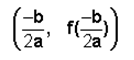
Las funciones cuadráticas son funciones polinómicas.

Ejemplo:

FUNCIÓN RACIONAL

Una función racional es el cociente de dos funciones polinómicas. Así es que q es una función racional si para todo x en el dominio, se tiene:

Nota: El dominio de una función polinómica son los números reales; sin embargo, el dominio de una función racional consiste de todos los números reales excepto los ceros del polinomio en el denominador (ya que la división por cero no está definida).

Función  de potencia

Una función de potencia es toda función de la forma  f(x) = xr, donde r es cualquier número real.

Las funciones f(x) = x4/3 y  h(x) = 5x3/2 son funciones de potencia.